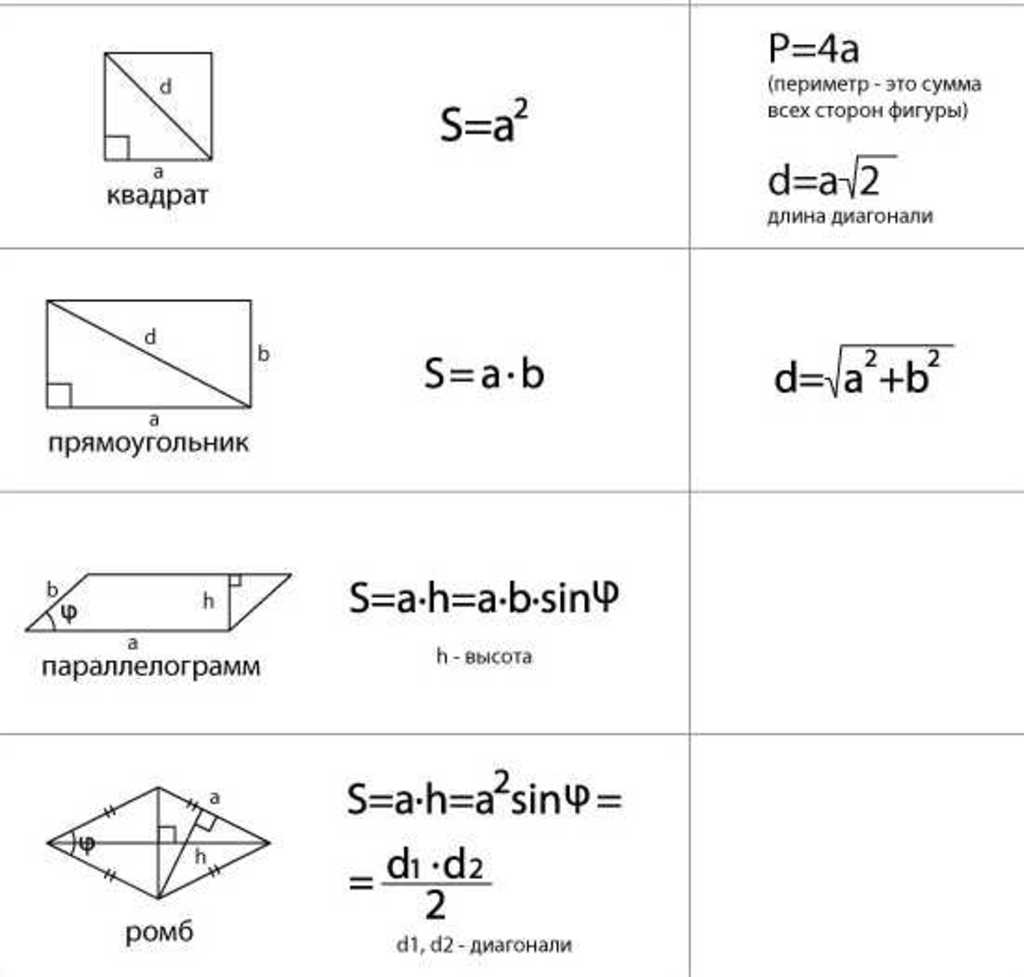
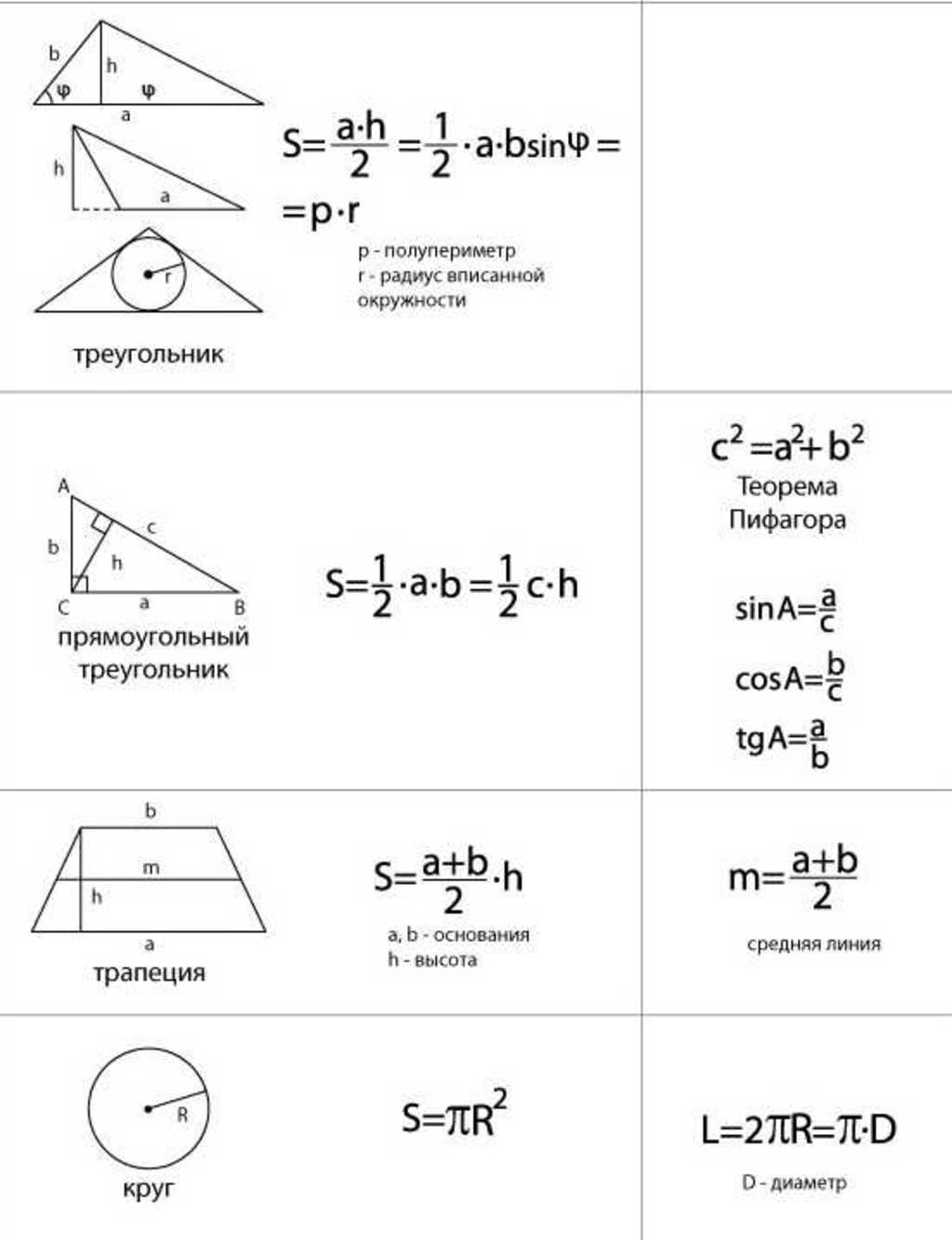
Задачи на нахождение площади фигур на клетчатой бумаге (задание В3 ЕГЭ)
Образовательный стандарт подразумевает, что выпускник средней школы должен:
- Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
- Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей).
Для этого, безусловно, нужно повторить определения и свойства геометрических фигур, которые вы изучали в школе, а также основные формулы из курса планиметрии. Задачи B3 из банка заданий ФИПИ, можно разделить на следующие типы:
- Задачи на формулы площади.
- Задачи на площадь фигуры на клетчатой бумаге.
- Задачи на площадь фигуры на координатной плоскости.
- Задачи на понятие координатной плоскости.
- Задачи на вектора.
Для решения задач на нахождение площади фигуры на клетчатой бумаге требуются знания формул площадей треугольников, параллелограммов, трапеций, круга и его частей, умения применять эти формулы для нахождения площадей фигур, находить площадь фигуры методом разбиения ее на более простые фигуры.
Способ 1
1) достроить фигуру до прямоугольника или прямоугольного треугольника
2) Найти S1 полученной фигуры (прямоугольника или треугольника)
3) Найти S2 добавленных частей
4) Вычесть S1 – S2 = получим S нужной фигуры.
Способ 2
Вычислить площадь можно не достраивая фигуру до новой фигуры, площадь которой можно вычислить по известным формулам, а разбив фигуру на части, площади которых можно легко найти и сложить площади частей.
Способ 3
1) ПО формуле – самый простой способ
Этот способ используется тогда, когда чётко видно, что за фигура и легко найти величины для вычисления S.